Technical Library

TEMPERAMENTS XXII: Neidhardt’s “Kleine Stadt” 1732

BAYERISCHEN STAATSBIBLIOTHEK

Titlepage of Neidhardt’s Gäntzlich erschöpfte…

Some musicians despise Vallotti’s popularity as a generic all-purpose temperament. Its nice symmetry, with six narrow fifths together on the sharp side of F and the remaining six fifths pure, gives an even gradation of key color. If you have been following these pages, though, you will know that a Major third derived from any chain of four pure fifths in a row is worse than Equal Temperament. If it were possible to somehow split the long chain of six pure fifths in Vallotti, perhaps something less grating could be obtained for the extreme keys. Like all temperaments, though, this must come at a cost.

The Juilliard Historical Performance program commenced in 2009, and this temperament, their stock-standard for ensembles, will probably spread worldwide as its graduates disperse from New York. I wonder, though, how many musicians are aware of the structure of this temperament, beyond dialing it up on their smart phone apps? A good number of the musicians I work with at Carmel Bach Festival each year come from the East Coast, and harpsichordist Dongsok Shin asked me to tune this temperament for several performances during Carmel Bach’s 80th season in 2017.

It would appear that Johann Georg Neidhardt (1680–1739) was somewhat of a temperament freak. In his Sectio Canonis Harmonici zur völligen Richtigkeit der Generum Modulandi of 1724 he went so far as to recommend which of his temperaments might be suitable for a village, a small city, a large city, or for making music in the Court itself—the latter in fact our familiar Equal Temperament. In the next decade, he provided monochord string lengths and discussed twenty-one temperaments in his Gäntzlich erschöpfte, Mathematische Abtheilungen des Diatonisch-Chromatischen, temperirten Canonis Monochordi etc. (The digitized original of a 1734 printing can be viewed online at the Bayerischen Staatsbibliothek website.)

The temperament we will consider here is Neidhardt’s Kleine Stadt from 1732. When talking about Neidhardt’s many temperaments, you have to be careful to note not only the name he gave them, but also the year: He changed his suggested use of many of them, and his ein Dorf (Village) from 1724 was upgraded to Kleine Stadt (Small City) in 1732.

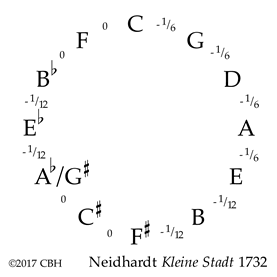
Observe that this Neidhardt temperament has two sizes of narrowed fifths: Four familiar sixth-comma fifths of Vallotti in a row from C to E, four twelfth-comma (equal-tempered) fifths in pairs, and four pure fifths also in pairs to complete the circle. Our job, as always, is to place each fifth correctly around the circle.

If you have just tuned Vallotti, several notes (C, G, D, A, E, F♯, C♯ and G♯) do not need to be moved: Only the four remaining pitches (F, B♭, E♭ and B) need to be retuned to change your temperament to Kleine Stadt 1732:

1. Lower your f until it makes a pure 5th with middle c', and tune up an octave to f'. (Instead of three beats a second for f–a in Vallotti, this increases the beat speed of that interval to five times a second.)

2. Lower your b♭ so it makes a pure fifth with f'.

3. Lower your e♭ to make an equal-tempered narrow fifth e♭–b♭, beating only about once every two seconds. Tune up an octave to e♭' and check a♭–e♭' which should now also be only slightly narrow, again an equal-tempered fifth.

4. Sharpen your b slightly to make your e–b equal-tempered. Check b–f♯' which should no longer be the pure fifth of Vallotti, but slightly narrow, again an equal-tempered fifth.

What have we accomplished musically? It’s certainly more bland sounding than Vallotti and we have lost Vallotti’s smooth progression of key color. No keys have improved, G Major is slightly worse, and the flat keys of F, B♭, E♭ Major are noticeably harsher.

To tune Neidhardt’s Kleine Stadt 1732 from scratch, we will setup a chain of narrow fifths like Vallotti or Young, although one of these pitches will only be temporary. Follow these instructions:

1. Tune your a' to a tuning fork, and tune a in absolute perfect tune a beatless octave below it.

2. Set the f a third below that a: Tune it pure first of all, but then widen the interval by flattening the f until you hear three distinct beats per second. This is only a temporary position for the f—we must eventually flatten it some more.

3. Using the temporary position of F, we are going to squeeze all the fifths in the circle between F and A by exactly the same amount, a sixth-comma. Tune middle c' pure to f, then narrow the interval by lowering your middle c' a little until you hear a lazy beat of a bit more than once a second.

4. Tune d' pure to a', then raise your d' a little, again squeezing the interval so it has a perceptible but not overly blatant wave. This interval will beat a tad less than twice per second, so check it against the second hand on your watch until you have a good wow-wow, wow-wow. It helps to replay the interval every second or so—listen when the notes are fresh so you don’t have to struggle to hear the beats while the sound is dying away.

5. Tune g a beatless fifth below d', then squeeze the interval by raising the g. Compare f–c' to g–d': These two intervals are the same size—the first only temporarily—so they should sound pretty similar for now. The f–c' fifth is a tone lower, so if your intervals are to be the same theoretical size, f–c' should beat marginally slower than g–d', but don’t fuss needlessly.

6. Tune g' up an octave from g. Compare c'–g' to d'–a': These two intervals are the same size, so again they should sound pretty similar. If not, a little error may have crept in, so juggle all these fifths until you are happy with their uniform roughness. Don’t move your a, nor your f just yet!

7. Tune e' pure to a, then lower it a little, squeezing the interval so it has a perceptible but not overly blatant wave. Compare g–d' to a–e'. Now drop down the octave from e' to e, which of course must be tuned pure. You have now completed a chain of five sixth-comma narrow fifths, although we will retain only four for this temperament.

8. Lower your f until it now makes a pure fifth below middle c', and tune up an octave to f'. Likewise, tune your b♭ a pure fifth below f'.

9. Now we will return to the sharp side of the circle. The diagram shows the two fifths on the sharp side of E are narrow, but by only a twelfth of a comma—same as an equal tempered fifth. Tune b pure above e, then lower the b a fraction. The fifth e–b will beat about only once every two seconds. Tune the fifth b–f♯' likewise, the f♯' pure above b first of all, then squeeze it. Compare b–f♯' to c–g' a semitone higher: The b–f♯' should beat about once a second, half the speed of c–g'. Tune down an octave to f♯.

10. Two more pure fifths come next: f♯–c♯' and c♯'–g♯'. Tune down an octave to find g♯.

11. Only one note remains. You must fit your E♭ in the circle between B♭ and A♭, so that both the fifths it makes are ever so slightly narrow, again equal tempered fifths. Tune your e♭ pure to b♭, then raise it to make make an equal-tempered fifth e♭–b♭, beating only about once every two seconds. Compare it to the same-sized interval e–ba semitone higher. Tune up an octave to e♭' and check a♭–e♭' which should now also be only slightly narrow.

Check and determine you have everything in the right place: For practical purposes in these types of temperaments, the proportion and location of the various-sized fifths is more important than absolute mathematical precision. There are four sixth-comma narrow fifths g–d', a'–e', c'–g' & d'–a' and four twelfth-comma narrow fifths e♭–b♭, f♯–c♯', b♭–f', & b–f♯'. (I’ve listed these in ascending order within both groups to help you hear the increasing beat speeds as you rise in pitch.) And don’t forget the four pure fifths f–c', f♯–c♯', b♭–f' & c♯–g♯'!

Further discussion
Anonymous [Kayano, Moxzan] Dodecagon — Chi-s akt temo Tokyo 2012, p94
Padgham, Charles The Well-Tempered Organ Positive Press, Oxford 1986, p71

	Pitch nomenclature
	Harpsichord Tuning Process
	Tuning Bibliography
	Technical Library overview
	Harpsichords Australia Home Page